The Earley algorithm is a top-down chart parser that parses natural language and does this very efficiently. Given a grammar that contains syntax rules and the words of a language, it parses a sentence into all possible syntax trees. The unification extension adds further restrictions to the syntax rules. An example of such a restriction is that the rule S => NP VP only applies if the number and person of the NP agrees with that of the VP. When NP is "The children", then the VP may be "are playing", but cannot be "is playing" (a restriction on number) or "am playing" (a restriction on person). The grammar should provide extra feature structures for the syntax rules. The unification extension of the Earley parser applies these structures and ensures that a sentence with a feature error will not be parsed.

I just provide the code to give you some idea and hints on to implement it. The code has not been tested very much since I just finished it. I place it under MIT license.

Earley parser source code

The algorithm may be found in the book "Speech and language Processing" (first edition), chapter 11, page 431. In the second edition of the book the algorithm may be found in chapter 15. The rest of this article presumes you have read it, since I cannot quickly repeat all the information given in chapter 11.

The book first describes the basic Earley algorithm, which can be found on Wikipedia. Some implementations are available there as well. It is described in chapter 10 of the book but can be hard to really understand it, because of the undescriptive use of variable names like A and B, and that it uses two functions that are not specified, NEXT-CAT and PARTS-OF-SPEECH.

Syntax rules and feature structures

For the basic algorithm I use syntax rules like the following S => NP VP

array(
    array('cat' => 'S'),
    array('cat' => 'NP'),
    array('cat' => 'VP'),
),

The same rule, extended with feature structures looks like this:

array(
    array('cat' => 'S', 'features' => array('head-1' => null)),
    array('cat' => 'NP', 'features' => array('head' => array('agreement-2' => null))),
    array('cat' => 'VP', 'features' => array('head-1' => array('agreement-2' => null))),
),

This implements the feature structure that is described on page 428 of the book:

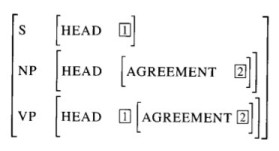
Features of the implementation

The implementation of the algorithm handles unification for syntax rules like this,

VP => NP NP

as described on the bottom of page 406. The rule as two identical consequents. If the grammatical categories of the rule are implemented as keys in a hashtable (as they are in my code) then they need to be discerned. I do that by adding the position of the category in the rule.

The book says: VP => NP(1) NP(2)

in the implementation it looks like this: VP@0 => NP@1 NP@2 (but you don't need to think about this when you write the syntax rules)

It also deals with rules like this NP => NP PP where one consequent is identical to the antecedent.

Remarks on the algorithm

The meaning of the function "FOLLOW-PATH" is not described in the book, but I presume that it means that it returns a subset of its argument. It starts out with the label "cat" and follows it to the end.

The function "UNIFY-STATES" of the original algorithm performed a "FOLLOW-PATH" of "dag2". I think this is an error in the algorithm, because it would corrupt the feature set of the charted state.

My version of unifyStates is also somewhat different since I take into account that a rule may have the same category at different positions (as in the VP => NP NP example).

Labeled DAGs

Unifying DAGs is a very elegant to implement unification. I could not follow the explanation of the unification process as described on page 423, unfortunately. That's why I decided to create a different implementation of this function. I introduced a class to separate the logic of the datastructure: LabeledDAG, a labeled directed acyclic graph (or DAG). Which reminds me to thank my employer at Procurios, Bert Slagter, for inadvertently providing me with a perfect datastructure for this task.

Finally

I also added the possibility to stop parsing when the first complete sentence is found. For some applications you are only interested in a single interpretation; it might as well be the first one, especially if you succeed to order your syntax rules in such a way that the best interpretation is found first.